Tl;dr — We look at some important concepts and examples of categories that will come up over and over again.

As a quick review, a category is a collection of objects with morphisms between them that can be composed together. Check out my previous post introducing categories if you need a refresher.

Preorders

Preorders are categories in which there is at most one morphism between any two objects. In our pictures of categories, this means there is at most one arrow from one object to another (there might be one going from $x$ to $y$ and one from $y$ to $x$ though).

Another way to think about preorders is that all parallel paths are equal. By a path we mean any sequence of arrows where the target of one arrow is the source of the next (so they can be composed together). By parallel paths we mean all the paths have the same initial sources and the same final targets. By all parallel paths are equal we specifically mean that the compositions of all the morphisms in each path are equal to each other.

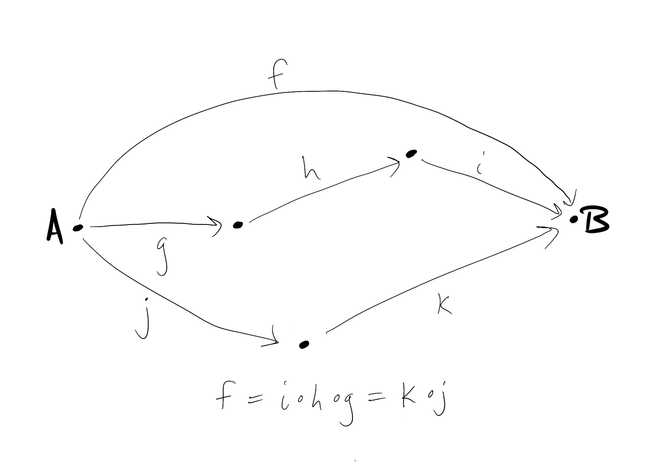
For preorders, we often denote that there is a morphism from an object $x$ to an object $y$ by writing $x ≤ y$.

The definition of a category implies that for any object $x$ we have $x ≤ x$, and for any three objects $x, y, z$, if $x ≤ y$ and $y ≤ z$, then $x ≤ z$.

I like to think of preorders as generalized hierarchies, as the examples below hopefully illustrate.

Examples of preorders

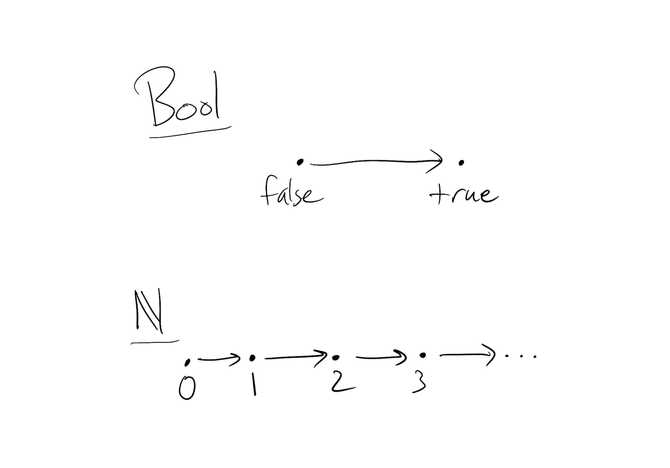
Bool

One of the simplest preorders is the booleans Bool = {false, true}. We get a preorder by setting false $≤$ true.

Natural numbers

The natural numbers $\mathbb{N}$ = {0, 1, 2… } form a preorder with the usual ordering $≤$ (e.g. 5 ≤ 9).

Resource theories

At a basic level, a resource theory is simply a collection of objects, or resources, a way to combine resources together as a single resource¹, and a way to convert resources to other resources, which corresponds to morphisms between resources.

We can think of resource theories as preorders if we set $x ≤ y$ if there is at least one morphism from $x$ to $y$.

An example is the set of all collections of atoms and molecules Mat (for materials). In Mat we denote combining materials by +, and a preorder structure is given by setting $x ≤ y$ if there is a chemical reaction that converts $x$ to $y$, which we usually write as $x \to y$ (note $\to$ is used instead of ≤ in this context).

Here’s a concrete example in Mat if the above doesn’t quite make sense:

This describes the chemical reaction creating water from hydrogen and oxygen.

Power sets

Given a set $S$, we can consider its power set $P(S),$ which is the set of all subsets of $S$. For example, if $S = \{a, b, c\},$ then

where $\{\}$ is the empty set.

We can turn $P(S)$ into a preorder as follows: if $X$ and $Y$ are subsets of $S$ (and thus elements of $P(S)$) we say $X ≤ Y$ if $X$ is a subset of $Y$, which following standard mathematical notation we write as $X \subseteq Y$.

Partial orders

Power sets are also examples of partially ordered sets, often abbreviated as posets. A poset is a preorder that has the additional property that if $x ≤ y$ and $y ≤ x$, then $x = y$. In other words, you can’t have arrows that form loops like the following diagram:

In terms of sets, if a set $X$ is a subset of $Y$, and $Y$ is a subset of $X$, then they must have exactly the same elements, and thus are the same set.

Posets are partially ordered in the sense that you don’t need to be able to compare every pair of objects. For example, say $S$ = {a, b, c}. Then {a} and {b} are subsets of $S$, but neither is a subset of the other, which is to say neither {a} $\nsubseteq$ {b} nor {b} $\nsubseteq$ {a}.

Total orders

Bool and $\mathbb{N}$ are also partial orders, and in fact they are also total orders. A total order is a poset for which every two objects are comparable, so either $x$ ≤ $y$ or $y$ ≤ $x$ is true (and if both are true then $x = y$).

Pictorially the objects of a total order can be placed in a line with all the arrows pointing in the same direction, as in our pictures of Bool and $\mathbb{N}$ above.

The category of sets

This is probably the most important category in mathematics, since sets come up all the time in mathematics. We denote this category by Set. The objects of Set are, as you might expect, all sets. The morphisms between them are functions between sets.

If you don’t remember, a function $f: X \to Y$ between sets $X$ and $Y$ is a relation that takes each element $x$ in $X$ to an element $y$ in $Y$, where we usually denote this mapping explicitly by writing $f(x)$ for $y$. Note that $f$ maps each $x$ to an $f(x)$ in $Y$, but for each $y$ there may or may not be an $x$ that maps to $y$ (in fact more than one $x$ could map to the same $y$).

Identity morphisms are given by the identity function: for any set $S$ define $id_S: S \to S$ by $id_S(s) = s$ for all $s$ in $S$.

Composition is also straightforward: for any two morphisms $f: A \to B, g: B \to C$ define their composite to be $g \circ f: A \to C$ by $(g \circ f) (a) = g(f(a))$ for all $a$ in $A$.

Monoids

Preorders are categories whose morphisms are simple: only one is allowed from one object to another. Monoids are like the reverse of preorders: there’s only one object, but there might be infinitely many morphisms.

Monoids might be more familiar in terms of sets: a monoid $M$ is defined to be a set with a binary operation $*: M \times M \to M$ that takes a pair $(m, m')$ of elements of $M$ and maps it to another element $m''$ of $M$. We write $m * m' = m''$. Note that in general $m * m' ≠ m' * m$.

There must also be an identity element $e$ in $M$ that satisfies $m * e = e * m = m$ for all $m$ in $M$. The operation $*$ must also satisfy an associativity property: $(m * n) * p = m * (n * p).$

From this description in terms of sets, do you see how to reconcile this with the category-theoretic definition of a monoid as a one-object category?

Here’s the answer: each element of $M$ corresponds to a morphism in the category, and in particular the identity element $e$ corresponds to the identity morphism $id$. The binary operation $*$ corresponds to composition of morphisms.

A common example of a monoid is strings in most programming languages: the empty string "" is the identity morphism, and string concatenation $+$ is composition.

We’ll talk about another important class of monoids after we introduce the idea of isomorphisms.

Isomorphisms

We often come across the idea that two objects $a$ and $b$ are not quite equal, but instead equivalent or interchangeable. They are equivalent in the sense that there exist morphisms $f: a \to b$ and $g: b \to a$ such that

We say that $f$ and $g$ are inverses of each other and write $f = g^{-1}$ and $g = f^{-1}$ to denote this. We also say that $a$ and $b$ are isomorphic, writing $a \cong b$, and that a morphism $h$ is an isomorphism if an inverse $h^{-1}$ exists.

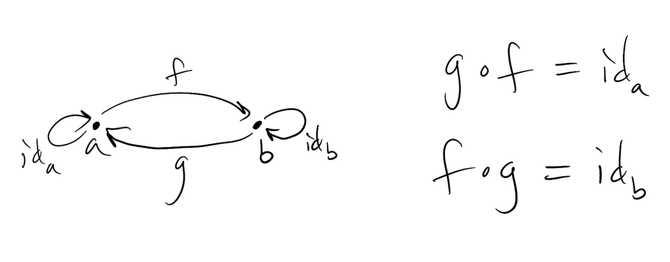
The intuition is that you can go from $a$ to $b$ through $f$ and then back to $a$ through $g$ (and similarly from $b$ to $a$ and back to $b$ through $g$ and then $f$), without losing any information.

As an example of losing information in Set, suppose $X = \{x, y\}$ and $Y = \{z\}$. Defining $f:X \to Y$ by setting $f(x) = f(y) = z$, we see there is no way to define an inverse function $g: Y \to X$ that satisfies $g(f(x)) = x$ and $g(f(y)) = y$ (that is, $g \circ f = id_X$). Going from $X$ to $Y$ we lose information about where we started from.

In a preorder, objects $a$ and $b$ are isomorphic if $a ≤ b$ and $b ≤ a$, and we can turn any preorder into a partial order by setting $a$ and $b$ equal to each other if $a \cong b$.

In the string monoid example above, the only isomorphism is the empty string with itself, since only "" + "" = "".

However, isomorphisms may not be unique. That is to say, there may be more than one isomorphism between a given pair of objects. For example, in Set, let $X$ = {a, b, c} and $Y$ = {1, 2, 3}. We can define an isomorphism by defining $f_1: X \to Y$ by $f_1(a) = 1, f_1(b) = 2, f_1(c) = 3$ and $g_1: Y \to X$ by $g_1(1) = a, g_1(2) = b, g_1(3) = c.$ You can check that $g_1 \circ f_1$ = $id_X$ and $f_1 \circ g_1$ = $id_Y$.

But we can define another isomorphism by defining $f_2(a) = 3, f_2(b) = 2, f_2(c) = 1$ and $g_2: Y \to X$ by $g_2(1) = c, g_2(2) = b, g_2(3) = a.$ Again you can check that $g_2 \circ f_2$ = $id_X$ and $f_2 \circ g_2$ = $id_Y$.

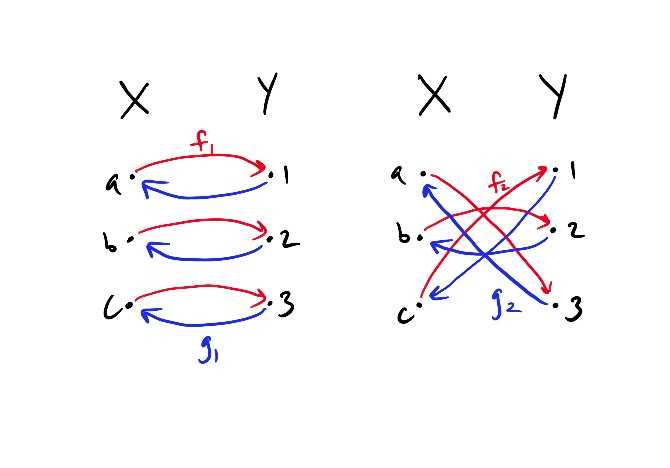
In fact there are a few more isomorphisms between $X$ and $Y$. How many are there?

Groups

Going back to our discussion of monoids, if every morphism of $M$ is an isomorphism, then $M$ is called a group.

Groups are super important, especially in physics. This is because groups generally have to do with symmetries, and symmetries are incredibly important.² Examples of symmetries include concrete ones like rotational symmetry and more abstract ones like the Lorentz symmetry of special relativity.

For each symmetry, there is a group associated with it. The morphisms of the group (viewed as a one-object category) correspond to the transformations that preserve the symmetry.

For example, rotating a square about its center by $90^{\circ}$ leaves it unchanged. In fact, there are seven more symmetry transformations of the square. Can you think of what they are? This group of symmetry transformations is known as the dihedral group of the square, usually denoted $D_4$.

I think it’s intuitive that groups are one-object categories, because each symmetry transformation only acts on a single object, and each transformation corresponds to a morphism from the (abstract) object in the category to itself. It’s basically an abstract picture of what’s happening.

The fact that each morphism is an isomorphism reflects the fact that the symmetry transformations are invertible: if I rotate by nintey degrees one way, I can undo it by rotating ninety degrees the other way.

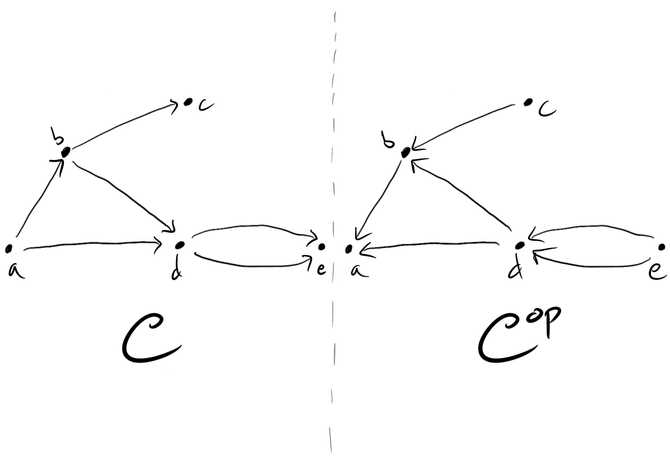
Opposite categories

Our last example of categories is that of opposite categories — given a category $C$, we get another one for free! We denote it by $C^{\text{op}}$ and call it the opposite category of $C$. It’s opposite in the sense that the objects of $C^{\text{op}}$ are the same as the objects of $C$, but the morphisms are reversed: if $f: a \to b$ is a morphism from $a$ to $b$ in $C$, then in $C^{\text{op}}$ $f$ is considered a morphism from $b$ to $a$ instead.

Composition remains the same, so that if $f: a \to b$ and $g: b \to c$, then in the opposite category $g \circ f$ becomes a morphism from $c$ to $a$.

For preorders, this is literally reversing all the arrows.