Tl;dr — We introduce functors, which allow us to relate different categories. As an applied example, we think of database schemas as categories and database instances as functors.

We often want to relate one category to another. Perhaps we see that one category is embedded inside of another one, or that we can simplify our view of a category by mapping it onto a less complex one, or that one category is in some sense the same as another one. Functors formalize these ideas. They’re like the mathematical version of analogies.

A functor $F$ from a category $\mathcal{C}$ to a category $\mathcal{D}$, written as $F: \mathcal{C} \to \mathcal{D}$, associates an object $F(c)$ in $\mathcal{D}$ for every object $c$ in $\mathcal{C}$ and a morphism $F(f): F(c_1) \to F(c_2)$ in $\mathcal{D}$ for every morphism $f: c_1 \to c_2$ in $\mathcal{C}.$

Furthermore, $F$ must respect the structure that defines a category, namely identities and composition. This means that

for every $c$ in $\mathcal{C}$ and that for any three objects $c_1, c_2, c_3$ and morphisms $f: c_1 \to c_2, g: c_2 \to c_3$ in $\mathcal{C}$,

in $\mathcal{D}$.

In plain words, these equations say that $F$ maps identity morphisms to identity morphisms and that a composition of two morphisms is mapped to the composition of the mappings of the two morphisms.

Examples of functors

Diagrams

Our pictures of categories, now referred to as diagrams, are in fact functors! Formally, a diagram $D$ of shape $\mathcal{J}$ in $\mathcal{C}$ is a functor $D: \mathcal{J} \to \mathcal{C}$.

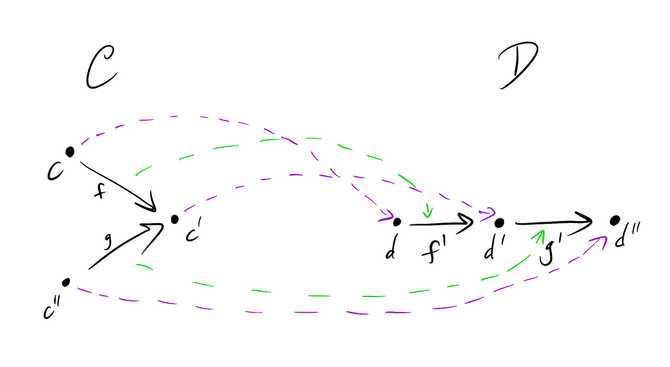
This definition really confused me when I first encountered it, until I realized that what we draw is the image of the functor. This is a lot like when we plot a function, say, the parabola $y = x^2$, we often say that the graph is the function. Here’s a picture that illustrates what I mean:

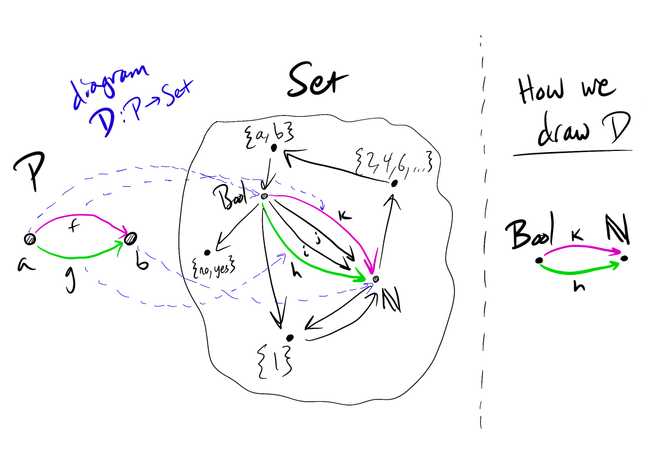
In this picture $P$ is a category with two objects $a$ and $b$ with two morphisms $f$ and $g$ that go from $a$ to $b$. I’ve also drawn a few sets in the category $\mathbf{Set}$¹ and a few arrows representing functions between them. We want a diagram $D$ of this shape relating $\mathbf{Bool}$ to $\mathbb{N}$. $D$ sends $a$ to $\mathbf{Bool}$ and $b$ to $\mathbb{N}.$ $D$ also selects two functions from $\mathbf{Bool}$ to $\mathbb{N}$ to map $f$ and $g$ to: $f$ to $k: \mathbf{Bool} \to \mathbb{N},$ and $g$ to $h: \mathbf{Bool} \to \mathbb{N}$.

To the right of the dotted line, I’ve drawn the image of the diagram $D$, which is what we would normally draw for $D$.

Isomorphic categories and a category of categories

Each category $\mathcal{C}$ has an identity functor $id_{\mathcal{C}}: \mathcal{C} \to \mathcal{C}$ which, as you might guess, takes each object to itself and each morphism to itself.

Our notation for identity functors and general functors between categories is really similar to the notation used for morphisms within a category. This is no coincidence.

We can define a category of categories by taking the objects to be categories and the morphisms to be functors between categories.

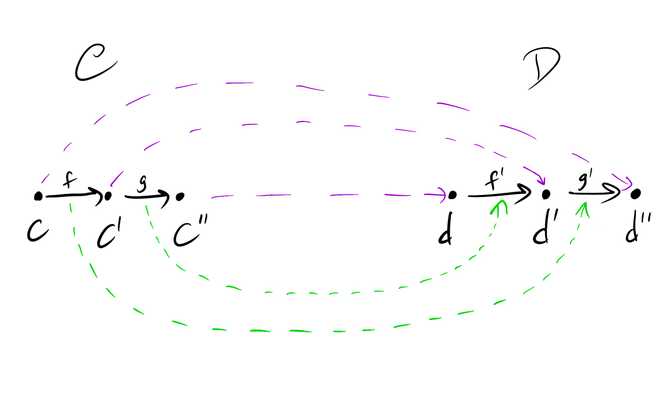
Composition of two functors $F: \mathcal{A} \to \mathcal{B}$ and $G: \mathcal{B} \to \mathcal{C}$ is given by the functor $G \circ F: \mathcal{A} \to \mathcal{C}$ defined by sending objects $a$ of $A$ to $G(F(a))$ and morphisms $f: x \to y$ of $\mathcal{A}$ to $G(F(f)): G(F(x)) \to G(F(y)).$

Following our discussion of isomorphisms in my last post, two categories $\mathcal{C}$ and $\mathcal{D}$ are isomorphic if there are functors $F: \mathcal{C} \to \mathcal{D}$ and $G: \mathcal{D} \to \mathcal{C}$ such that

Isomorphic categories have exactly the same structure.

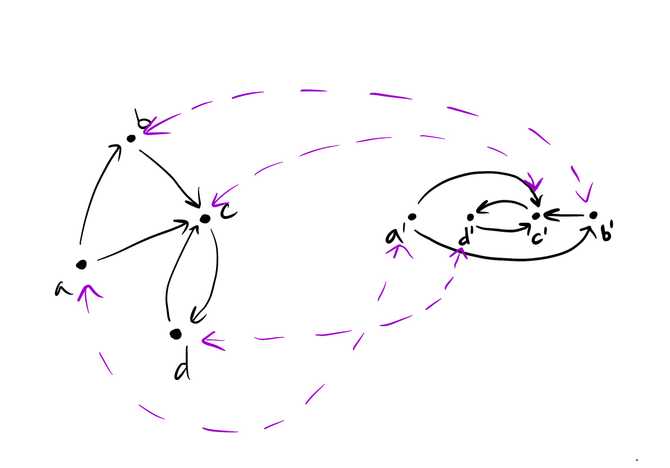
Embedding one category within another

Going from a smaller category $\mathcal{C}$ to a larger category $\mathcal{D}$ (in terms of objects), we can think of a functor as embedding $\mathcal{C}$ in $\mathcal{D}$ if no information is lost, i.e., no objects or morphisms in $\mathcal{C}$ are collapsed together in $\mathcal{D}$.

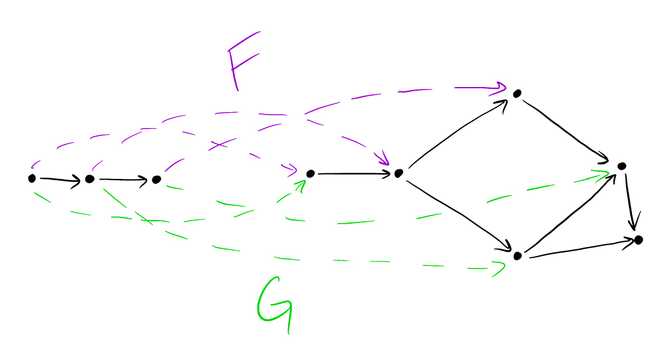
Collapsing categories

Example from Bool to Set

Recall $\mathbf{Bool}$ is the two-element preorder given by false $≤$ true. We can define a functor $F: \mathbf{Bool} \to \mathbf{Set}$ by $F(\text{false}) = F(\text{true}) = [0, 1]$ where $[0,1]$ is the set of all real numbers in between and including 0 and 1. $F$ sends $≤: \text{false} \to \text{true}$ to $f: [0, 1] \to [0,1]$ defined by $f(x) = x^2$ for all $x$ in $[0, 1].$

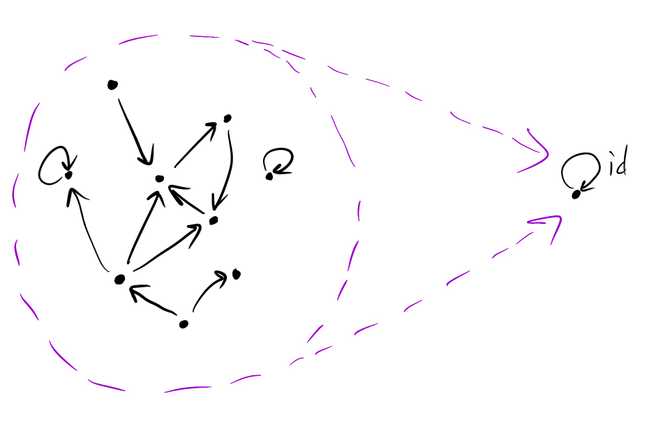
Constant functors

An extreme case is a constant functor, which maps all objects to a single object $c$ in the target category and all morphisms to the identity morphism $id_c$.

Nonexamples of functors

In the picture below, on the left we have a preorder $\mathcal{C}$ that consists of three objects $c, c', c''$ where both $c$ and $c''$ are $≤ c'$ (the corresponding arrows are labeled $f$ and $g$). On the right is a preorder $\mathcal{D}$ with three objects $d, d', d''$ where $d ≤ d' ≤ d''$ (the corresponding arrows are labeled $f'$ and $g'$).

I’ve also drawn a mapping of objects and morphisms of $\mathcal{C}$ to $\mathcal{D}$ which is not a functor. The mapping respects the direction of $f$, but it reverses the direction of $g$, in the sense that $g$ has source $c''$, which maps to $d''$, and target $c'$, which maps to $d'$, but $g$ is mapped to $g'$ which has source $d'$ and target $d''$.

As we just saw, if a mapping of categories from $\mathcal{C}$ to $\mathcal{D}$ reverses morphisms, then the mapping can’t be a functor… unless it reverses all the morphisms, in which case it could be a functor from the opposite category $\mathcal{C}^{\text{op}}$ to $\mathcal{D}$ (as long as it preserves identities and composition of course). Such a functor is known as a contravariant functor. A regular functor is referred to as a covariant functor.

An application: database schemas and instances

A database schema $\mathcal{C}$ is essentially a finitely-presented category with path equations.

By finitely-presented category, we mean that the category is obtained by interpreting a finite graph as a category (taking vertices as objects and arrows as morphisms), and any relationships between morphisms (often thought of as constraints or business rules) are given by path equations.

Here’s an example schema for a university that is pretty self-explanatory:

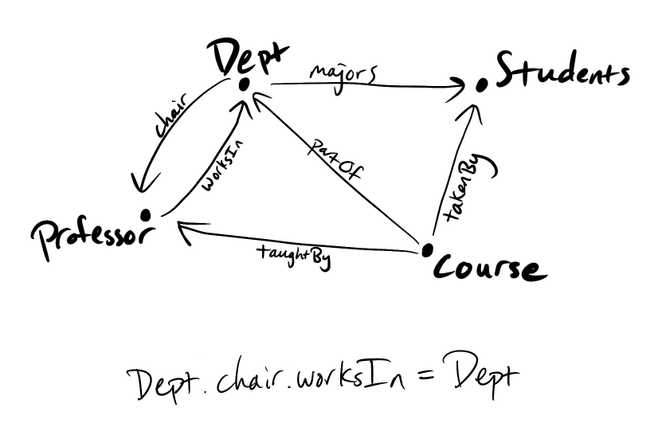
We have a constraint Dept.chair.worksIn = Dept, which says that the chair of a department works in that department. This constraint leads to other constraints, like Professor.worksIn.chair.worksIn.chair = Professor.worksIn.chair, which amounts to saying that a professor’s department chair’s chair is themself.

An instance (in time) of a database schema $\mathcal{C}$, i.e., actual data, is a functor from $\mathcal{C}$ to Set. One way to think about this is that the schema is the abstract structure, and the functor is a representation of that structure in the form of concrete data.

Here is a schema $\mathcal{C}$:

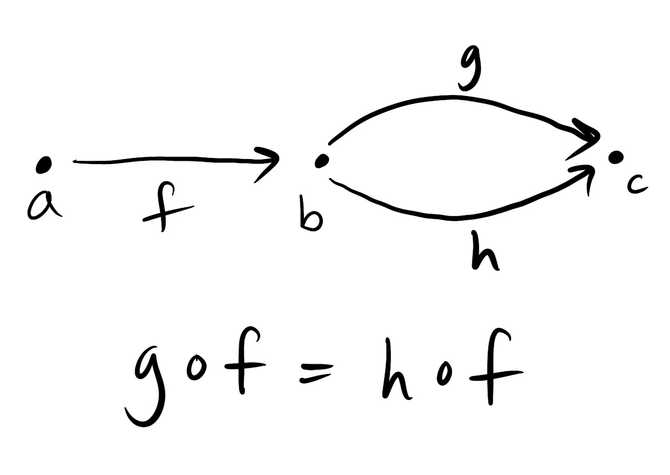
We can give this a concrete representation as a database instance by defining a functor $F: \mathcal{C} \to \textbf{Set}$ by setting $F(a)$ to be the set of all college students in the US, $F(b)$ to be the set of all students at a given university $X$, and $F(c)$ to be the power set of all courses at $X$.

$F(f)$ selects out the all students at the university $X$ who got all A’s, $F(g)$ maps students at $X$ to the courses they’re taking, and $F(h)$ maps students at $X$ to the courses they got at least a B in.

If we first filter by the students that get an A in all their courses, then those students’ courses are the same as the courses that they at least got a B in. In other words, $F(g) \neq F(h)$, but $F(g) \circ F(f) = F(h) \circ F(f)$.

Graphs as database instances

We can even view graphs as database instances of the schema given by the category $\mathbf{Gr}$:

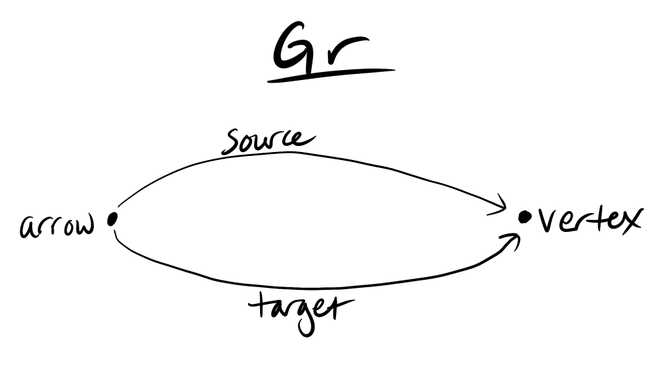
$\mathbf{Gr}$ has two objects, one labelled $\text{arrow}$ and one labelled $\text{vertex}$. There are two morphisms from $\text{arrow}$ to $\text{vertex}$ labelled $\text{source}$ and $\text{target}$.

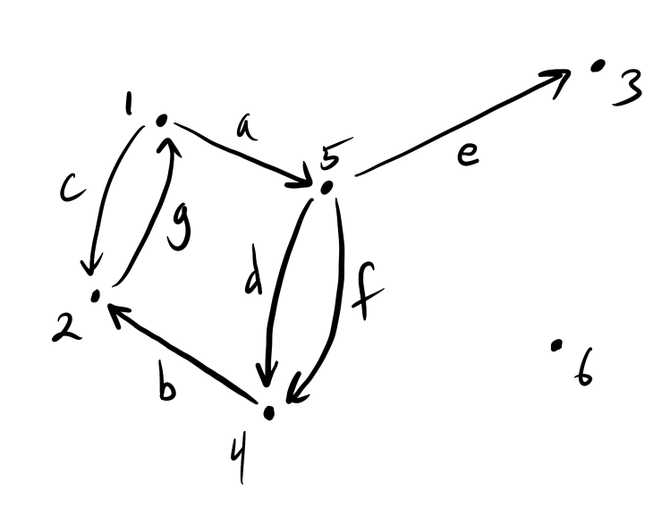
As an example, we can view the graph $G$ pictured below as a functor $G: \mathbf{Gr} \to \mathbf{Set}$, where $G(\text{vertex}) = \{1, 2, 3, 4, 5, 6 \}$, $G(\text{arrow}) = \{a, b, c, d, e, f, g \}$ where

$G(\text{source})$ maps each arrow to its source vertex, and $G(\text{target})$ maps each arrow to its target vertex.

As is discussed in Seven Sketches in Compositionality, you can use functors between database schemas to create special functors to migrate data. The benefit is that you can reason with them and prove that a data migration won’t fail.

Do functors form categories?

Functors relate categories to one another, but can we also think of functors forming their own categories? The answer is yes, and categories whose objects can be interpreted as functors are known as functor categories.

But what are the morphisms in such a category? How do we relate one functor to another? This will be the topic of my next category theory post — natural transformations.

References

See chapter 3 of Seven Sketches in Compositionality for much more detail on all of the topics covered here and more.